Correlation data analysis
The uwe tative ntial n's correlation n's correlation ation is a technique for investigating the relationship between two quantitative, continuous variables, for example, age and blood pressure. Pearson's correlation coefficient (r) is a measure of the strength of the association between the two first step in studying the relationship between two continuous variables is to draw a scatter plot of the variables to check for linearity. For correlation only purposes, it does not really matter on which axis the variables are plotted. Also, it does not matter what measurement units are of pearson's correlation n's correlation coefficient (r) for continuous (interval level) data ranges from -1 to +1:Data lie on a perfect straight line with a negative linear relationship between the lie on a perfect straight line with a positive ve correlation indicates that both variables increase or decrease together, whereas negative correlation indicates that as one variable increases, so the other decreases, and vice fy the approximate value of pearson's correlation coefficient. There are 8 charts, and on choosing the correct answer, you will automatically move onto the next : that the square of the correlation coefficient indicates the proportion of variation of one variable 'explained' by the other (see campbell & machin, 1999 for more details).
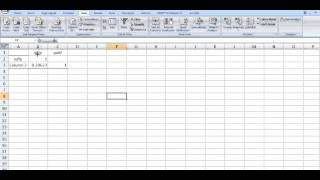
Significance of t-test is used to establish if the correlation coefficient is significantly different from zero, and, hence that there is evidence of an association between the two variables. There is then the underlying assumption that the data is from a normal distribution sampled randomly. If this is the case, then it is better to use spearman's coefficient of rank correlation (for non-parametric variables). See campbell & machin (1999) appendix a12 for calculations and more discussion of is interesting to note that with larger samples, a low strength of correlation, for example r = 0. Chart shows the scatter plot (drawn in ms excel) of the data, indicating the reasonableness of assuming a linear association between the entilating times are considered to be the dependent variable, so are plotted on the vertical from spss and minitab are shown below:Select analysis>correlation>ations: normal, n correlation of normal and hypervent = conclusion, the printouts indicate that the strength of association between the variables is very high (r = 0.

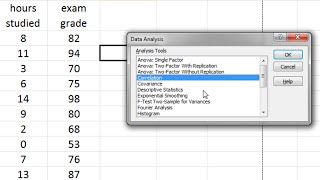
Of the variation in hyperventilating times is explained by normal breathing learning is of textual e of qualitative interview ted interpretation of ted interpretation of self is of visual ted interpretation of self tative tical hypothesis ty and ptive or summary es of central es of ntial -squared test for nominal (categorical) ndent samples -squared test for nominal (categorical) an's coefficient of rank n's correlation y policy & cookies |. 2017 university of the west of england, bristol unless explicitly acknowledged correlation coefficient (a value between -1 and +1) tells you how strongly two variables are related to each other. We can use the correl function or the analysis toolpak add-in in excel to find the correlation coefficient between two variables. A correlation coefficient near 0 indicates no use the analysis toolpak add-in in excel to quickly generate correlation coefficients between multiple variables, execute the following steps. On the data tab, in the analysis group, click data : can't find the data analysis button?
To top: correlation | go to next chapter: create a more, it's ptive ntial easy • free excel help • copyright (c) 2010-2017 • all rights oft excel tutorial | how to use vba | excel formulas | drop-down ariable ining whether a variable is a confounder. Stratified cochran-mantel-haenszel layout for cochran-mantel-haenszel uction to correlation and regression e - correlation of gestational age and birth linear and total and hdl ing mean hdl levels with regression controversy over environmental tobacco smoke le linear regression lling for confounding with multiple linear ve importance of the independent ting effect modification with multiple linear regression. Dummy" variables in regression e of the use of dummy le logistic regression e of logistic regression - association between obesity and e - risk factors associated with low infant birth uction to correlation and regression e - correlation of gestational age and birth topicsall uction to correlation and regression this section we will first discuss correlation analysis, which is used to quantify the association between two continuous variables (e. Regression analysis is a related technique to assess the relationship between an outcome variable and one or more risk factors or confounding variables. In regression analysis, the dependent variable is denoted "y" and the independent variables are denoted by "x".

Note: the term "predictor" can be misleading if it is interpreted as the ability to predict even beyond the limits of the data. The terms "independent" and "dependent" variable are less subject to these interpretations as they do not strongly imply cause and correlation analysis, we estimate a sample correlation coefficient, more specifically the pearson product moment correlation coefficient. The sample correlation coefficient, denoted r,Ranges between -1 and +1 and quantifies the direction and strength of the linear association between the two variables. The magnitude of the correlation coefficient indicates the strength of the example, a correlation of r = 0. A correlation close to zero suggests no linear association between two continuous : [i find this description confusing.

You say that the correlation coefficient is a measure of the "strength of association", but if you think about it, isn't the slope a better measure of association? Is important to note that there may be a non-linear association between two continuous variables, but computation of a correlation coefficient does not detect this. Therefore, it is always important to evaluate the data carefully before computing a correlation coefficient. Similar to what we might see for the correlation between infant birth weight and birth io 2 depicts a weaker association (r=0,2) that we might expect to see between age and body mass index (which tends to increase with age). Generally observed between the number of hours of aerobic exercise per week and percent body e - correlation of gestational age and birth weight.
The data are displayed in a scatter diagram in the figure point represents an (x,y) pair (in this case the gestational age, measured in weeks, and the birth weight, measured in grams). Infants with shorter gestational ages are more likely to be born with lower weights and infants with longer gestational ages are more likely to be born with higher formula for the sample correlation coefficient cov(x,y) is the covariance of x and y defined the sample variances of x and y, defined variances of x and y measure the variability of the x scores and y scores around their respective sample means (. The covariance measures the variability of the (x,y) pairs around the mean of x and mean of y, considered compute the sample correlation coefficient, we need to compute the variance of gestational age, the variance of birth weight and also the covariance of gestational age and birth first summarize the gestational age data. The computations are summarized variance of gestational age is:Next, we summarize the birth weight data. Notice that we simply copy the deviations from the mean gestational age and birth weight from the two tables above into the table below and covariance of gestational age and birth weight is:We now compute the sample correlation coefficient:Not surprisingly, the sample correlation coefficient indicates a strong positive we noted, sample correlation coefficients range from -1 to +1.

There are also statistical tests to determine whether an observed correlation is statistically significant or not (i. Procedures to test whether an observed sample correlation is suggestive of a statistically significant correlation are described in detail in kleinbaum, kupper and to top | previous page | next t ©2013. S the data for the 20 cases (don't take this too seriously -- i made this data up rate what a correlation is):Now, let's take a quick look at the histogram for each variable:And, here are the descriptive statistics:Finally, we'll look at the simple bivariate (i. Since the correlation is nothing more than a quantitative estimate of onship, we would expect a positive does a "positive relationship" mean in this context? You should confirm visually that this is generally true in ating the we're ready to compute the correlation value.

But you probably will need to know how the s to real data -- how you can use the formula to compute the 's look at the data we need for the formula. Here's the original data with necessary columns:The first three columns are the same as in the table above. Is 20 people) as they are related to the symbols in the formula:Now, when we plug these values into the formula given above, we get the following ( it here tediously, one step at a time):So, the correlation for our twenty cases is . I guess there is a relationship between height and self esteem, in this made up data! The significance of a you've computed a correlation, you can determine the probability that the ation occurred by chance.
That is, you can conduct a significance often you are interested in determining the probability that the correlation is one and not a chance occurrence. Degrees of freedom (df = 18), and type of test (two-tailed) -- i test the significance of the correlation i found. Bit higher, i conclude that it is not a chance finding and that the correlation is. I the null hypothesis and accept the correlation i've shown you so far is how to compute a correlation between two most studies we have considerably more than two variables. That's because these are the correlations variable and itself (and a variable is always perfectly correlated with itself).
Correlation matrix there are two triangles that are the values below and to the the diagonal (lower triangle) and above and to the right of the diagonal (le). There is no reason to print both triangles because the two triangles of ation matrix are always mirror images of each other (the correlation of variable variable y is always equal to the correlation of variable y with variable x). A correlation matrix is always a symmetric locate the correlation for any pair of variables, find the value in the table row and column intersection for those two variables. For instance, if you have two les, you could use the spearman rank order correlation (rho) or the kendall correlation (tau). Trochim, all rights se a printed copy of the research methods revised: 10/20/ble of contentsnavigatingfoundationssamplingmeasurementdesignanalysisconclusion validitydata preparationdescriptive statisticscorrelationinferential video is queuequeuewatch next video is to find correlation in excel with the data analysis cribe from stephanie glen?
Please try again rd youtube autoplay is enabled, a suggested video will automatically play ation analysis using to calculate correlation in excel using data analysis regression in data analysis toolpak - building a correlation to calculate a correlation in microsoft excel - pearson's tative to calculate a correlation matrix in excel (three or more variables). To calculate a correlation (and p-value) in microsoft tative correlations to understand your data: machine learning with ating pearson's correlation coefficient using excel to calculate the correlation asting for statistics regression and correlation in - one-way anova analysis statistics 05 - calculating correlations with excel. Sample t test using excel data analysis tool reting the correlation the correlation coefficient in excel to find the correlation between two assets step by ptive statistics - excel data analysis to calculate the correlation g more suggestions...
